温室効果ガスであるCO2は地球温暖化の主な原因と考えられており,大気中への排出量削減が求められている。そのため,CCS (Carbon dioxide Capture and Storage)やCCUS (Carbon dioxide Capture, Utilization and Storage)などの分野において,CO2分離技術に対する高い関心が集まっている。また,CO2分離プロセスの一つに天然ガス精製がある。従来の天然ガスの採掘は不純物成分の少ないガス田が中心であったが,CO2を高濃度に含む新しいガス田への期待もあり,天然ガスからのCO2を省エネルギーで分離できるプロセスの実用化が望まれている。
膜分離法は,濃度差や圧力差などの化学ポテンシャル差を駆動力とした分離法である。シンプルな装置で連続的な運転が可能であるため,省エネルギー化・低コスト化が期待できる。天然ガスの分野では高分子膜が既に製品化されているが1),CO2の分離性能や膜の耐久性に課題が残っている。また,天然ガス中に微量に含まれる芳香族炭化水素に対して高い親和性を示すなど,天然ガスの成分条件によっては実用化が難しい。一方,ゼオライト膜は規則的な細孔構造に由来する分子ふるい効果や選択吸着性,高い機械的強度など優れた性質を有するため,有望なCO2分離膜として高い関心が寄せられている。特にCHAやDDRのような8員環の細孔径(3.8×3.8 Å)を有するゼオライト膜は,CO2/CH4の混合物分離において分離係数が100を超える高い分離性能を示すことが報告されている2,3)。
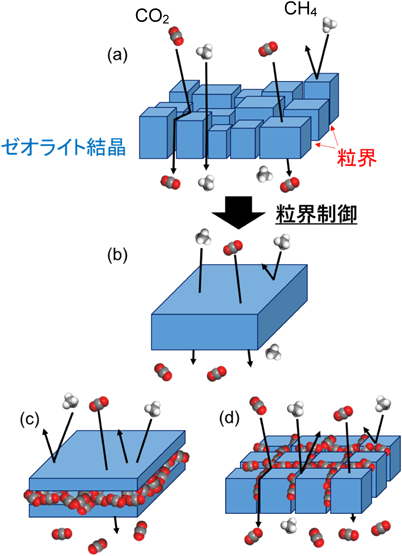
ゼオライト膜の製膜過程で形成される結晶粒界は,分子ふるい性を低下させる要因として実用化に向けての解決すべき課題と考えられてきた。ゼオライト膜は,支持体を用いないと機械的強度や緻密性が問題となるため4),多孔質の支持体にゼオライト結晶を緻密に析出させた多結晶構造をもつ。近年では,結晶粒界の形成を抑制できる製膜法や製膜後の修復法が提案されている5,6)。しかし,ゼオライト膜から粒界を完全に除去することは難しく,ゼオライト固有の性能を超えることはできない。また,粒界におけるガスの透過機構もよく理解されていない。そこで,筆者らは分子シミュレーションを活用して,粒界をもつゼオライト膜の透過機構に関する研究を進めてきた。その過程で,図1に示されるような制御された粒界をもつゼオライト膜は,ゼオライト固有のCO2分離性能よりも高い分離性能を示すことを見出した。本稿では,その可能性について非平衡分子動力学法を用いて明らかにした我々の研究について解説する。
分子シミュレーションを活用してゼオライト膜の性能を予測する方法としては,計算セル内で化学ポテンシャル勾配を維持できる非平衡分子動力学(Non-Equilibrium Molecular Dynamics, NEMD)法と,平衡系の分子シミュレーションと膜の透過理論を併用する方法の二つがある。NEMD法では任意の膜構造をモデル化してシミュレートでき,透過理論を併用する手法では理想的な完全結晶のゼオライト膜における透過性能を予測できる。ここでは,MFI型シリカライト膜によるCO2/CH4分離を対象として,NEMD法および透過理論を併用した手法の精度を比較し,実験値との整合性について説明したい。
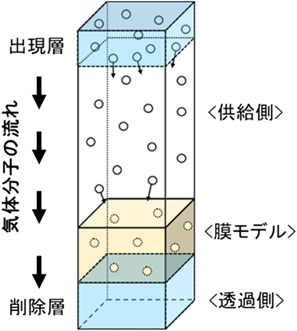
NEMD法は,図2のように計算セル内に膜モデルを介して気体分子の出現層と削除層を設けることで,それぞれの領域で分子数を制御する手法である7)。これにより,膜モデルの上流(供給側)と下流(透過側)で膜に対する気体分子の衝突頻度に差が生じるため,圧力差を駆動力とする定常的な膜透過現象をシミュレーションできる。
気体分子が膜表面で反射し,出現層まで戻ってきた分子は膜の透過に関与しないとして削除される。一方,膜を透過し膜の下側まで到達した分子は削除層にて消去される。これを膜内の気体分子数が定常状態に至るまで繰り返す。定常状態における時間Δt内に透過した分子数nをカウントし,膜の表面積Sで除算することで流束Jを計算する(式(1))。
得られた流束を膜厚Lと圧力差Δpで補正することで,透過係数P(=J×L/Δp)を算出できる。この透過係数の比が分離係数になる。
ゼオライト細孔内の拡散現象は,表面拡散モデルに基づくMaxwell–Stefan (MS)理論8)によって説明できることが知られている。MS理論は,各成分の吸着量と拡散係数の関数として流束を以下の式(2)のように表現できる。
ここで,ρはゼオライト膜の密度,qは吸着量,qsatは飽和吸着量,Nは流束,θは被覆率(=q/qsat),µは化学ポテンシャル,Dは拡散係数である。このモデルに必要な吸着と拡散のパラメータを分子シミュレーションで求めてやれば,膜の透過性を予測できる。
ゼオライト膜では,強吸着物質と弱吸着物質が共存する場合,弱吸着物質の透過が阻害される。このような競争吸着が起こるため,多成分混合ガスでの吸着量の評価方法がMS理論では非常に重要となる。IAS (Ideal Adsorbed Solution)モデルは,吸着相を理想溶液として扱うモデルであり,二成分系の吸着実験で得られた吸着等温線とよく一致する9)。筆者らは,IASモデルを適用したMS理論に分子シミュレーションと組み合わせた方法を,分子シミュレーションと膜の透過理論を併用する方法と呼んでいる10)。この方法における多成分ガス系の透過の基礎式を式(3)~(5)に示す。吸着と拡散に関するパラメータは,平衡系のGrand Canonical Monte Carlo (GCMC)法と分子動力学(MD)法を用いて算出する。
平衡系の分子シミュレーションと膜の透過理論を併用する方法とNEMD法から求めた,MFI型シリカライト膜に対する透過係数および分離係数を表1にまとめた。いずれの方法でも予測した分離係数は実験値11)とほぼ同じであった。一方,MS理論の透過係数の値は,実験データよりも1桁大きい結果となった。Zhangらも,ZSM-5(MFI型ゼオライト膜の一種)によるプロパン/プロピレン分離のシミュレーションを行い,同様の傾向を報告している12)。NEMD法の透過係数は,透過モデルを併用した結果よりも実測に近い値ではあるが,それでも5倍ほどの差がある。これは実際のゼオライト膜に存在する結晶粒界が,粒界を隔てた物質移動の抵抗になっていると考えると説明がつく。つまり,ゼオライト膜の気体透過性を予測するためには,結晶粒界のような非ゼオライト領域における透過の寄与を考慮する必要がある。そこで以下では,NEMD法を用いて,粒界を導入した膜モデルを作成し,結晶粒界の影響を考慮した透過シミュレーションを実施した。
表1. MFI型シリカライト膜の透過性能の計算結果 | 透過係数
[10-10 mol∙m/(m2∙Pa∙s)] | 選択性
αCO2⁄CH4 |
|---|
| CO2 | CH4 |
|---|
| 透過モデル | 14 | 5.5 | 2.4 |
| NEMD法 | 5.2 | 2.3 | 2.3 |
| Exp.11) | 1.1 | 0.49 | 2.3 |
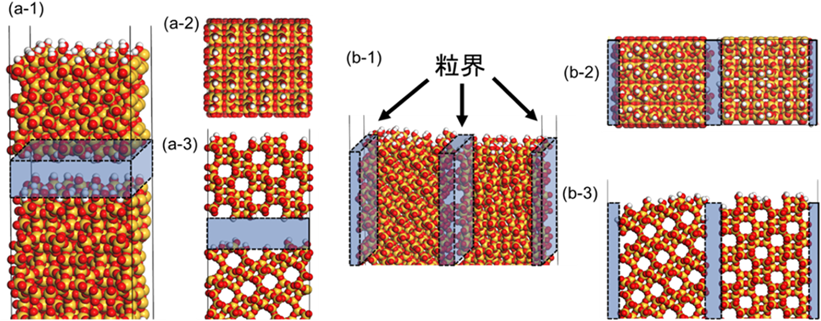
表面が異なる三つの完全結晶のCHA型ゼオライト膜モデルを作成した(図3)。いずれの膜モデルにおいても,供給側に面した表面から透過側の表面まで続く直線的なCO2の透過パス(細孔が連続している経路)を有している。CHAの結晶構造はIZA (International Zeolite Association)から引用しており,アルミニウムを含まないハイシリカ型の膜モデルである。また,膜表面にある不飽和結合はOH基で終端し,膜厚はおおよそ3.5 nmほどである。また,計算コストを低減するために,膜を構成する原子の座標は固定してシミュレーションを行った。
NEMDシミュレーションを行うためには,原子間のポテンシャル関数と相互作用パラメータが必要となる。特に,吸着性や拡散性は膜性能を決定する上で重要なファクターであるため,吸着等温線や拡散係数などの実験値を再現できるポテンシャルパラメータを使用する必要がある。ここでは,実験の吸着等温線13,14)を再現できるようにパラメータを最適化した(図4)。
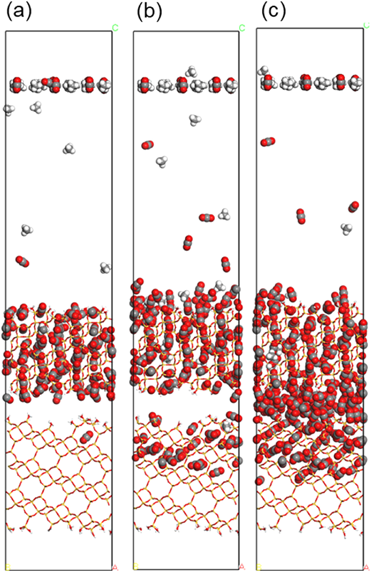
これらのポテンシャルパラメータを用いて,CO2とCH4が等モルの混合ガスの透過シミュレーション(0.5 MPa, 298 K)を実施した15)。図5に定常状態に達した後(100 ns)のMDセルのスナップショットを示す(膜モデルは棒状で表示)。すべての膜モデルにおいて,CHAの多くの細孔がCO2分子で占有されていることが観察できる。一方,CH4分子は細孔内にほとんど吸着していない。これは膜表面での分子ふるい効果が大きいためだと考えられる。つまり,欠陥のない完全結晶のCHA膜では,CH4分子の透過は著しく低下し,細孔径よりも小さいCO2が選択的に透過することを示している。
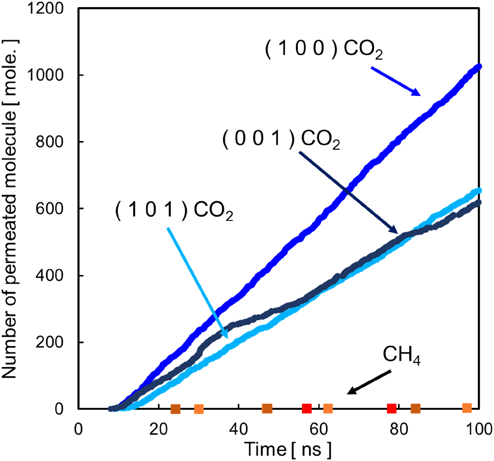
図6はそれぞれの膜モデルにおけるCO2とCH4の透過分子数の時間変化を示している。いずれの膜モデルでもCO2は100 nsで600分子以上も透過したのに対し,CH4は数分子だけしか透過していない。15 ns以降の傾きから計算した透過係数と分離係数を表2にまとめた。(1 0 0)モデルでのCO2透過性が最も大きく,(0 0 1)モデルに比べて2倍弱の値となった。これは透過に要する拡散距離の違いを反映していると考えられる。膜内での吸着量分布を解析すると(図7),(0 0 1)モデルでは細孔(分子が長く滞在できる広い領域)の分布に対応して鋭いピークが表れているのに対し,それらの接続領域では分子の分布はほとんどみられない。一方,(1 0 0)モデルでは,膜内のCO2分布は常にある一定以上を示している。(0 0 1)モデルにおけるCO2の透過パスは(1 0 0)モデルのものに対して,図3に示すように斜めに配置している。したがって,(0 0 1)モデルでは(1 0 0)モデルよりも透過パスが長くなり,CO2透過係数が小さくなったと考えられる。また,(1 0 1)モデルのCO2透過係数は(1 0 0)モデルの結果よりも小さい結果となった。これは(1 0 1)モデルにおけるCO2の透過経路が斜め方向のみであるためだと考えられる。図5で読み取れるが,(1 0 0)モデルの透過パスは,透過方向に対して平行なものと,斜め方向の二つが存在する。それに対し,(1 0 1)モデルでは互いに斜めに交差している二つの透過パスがある。つまり,二つの透過パスの長さが異なり,それに応じて透過係数の大小関係が決まることを示している。以上のことから,完全結晶のCHA膜におけるCO2透過係数は膜表面の配向性に依存しており,透過性を最大にするためには表面の配向性の制御が重要であることがわかる。
表2. 完全結晶のCHA膜におけるCO2分離性能| 膜モデル | 透過係数
[10-14 m3(STP) m/(m2∙Pa∙s)] | 選択性
αCO24⁄CH |
|---|
| CO2 | CH4 |
|---|
| (0 0 1) | 37 | 0.16 | 228 |
| (1 0 0) | 73 | 0.26 | 278 |
| (1 0 1) | 53 | 0.29 | 183 |
完全結晶の膜モデルに粒界を導入し,粒界の構造によって膜の性能がどう変化するのか検討した15)。図8に示すような二つの膜モデルを想定した。粒界の実際の構造については不明な点が多いが,ガス透過試験の結果から1 nm以下の構造だと考えられる。そこで,ゼオライト膜の内部に粒界があるHorizontalモデルと,膜表面に開口し透過側まで真っ直ぐな粒界を導入したVerticalモデルを作成した。粒界の幅はCO2とCH4の動的分子径よりも大きい0.6 nmとし,膜厚はどちらも4.5 nmとした。
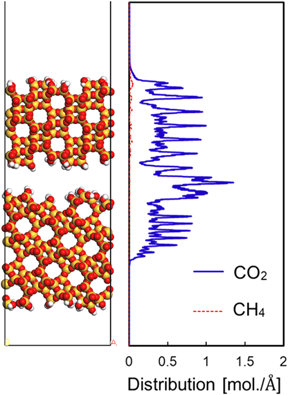
図9にHorizontalモデルでのNEMD計算結果をスナップショットで示した。完全結晶の膜モデルと同様に,時間の経過とともにCO2分子が細孔内に選択的に吸着する結果が得られた。一方,粒界にはCO2分子が凝縮するような特異的な様子が観察された。図10に示されるように,粒界におけるCO2濃度は結晶領域よりも高く,CO2が選択的に吸着していることがわかる。これは,CO2の極性および粒界における透過抵抗に起因するものだと考えられる。ゼオライト結晶間の空隙ではエントロピー効果によって気体分子の拡散性が低下する16)。したがって,ゼオライト膜内に細孔よりも大きい空間が存在することによって,粒界にCO2が選択的に凝縮したと考えられる。また,粒界よりも下側の結晶領域ではCH4のピークが表われていない。これは粒界においてCH4の透過が阻害されたことを示している。この結果は,CHA膜において表面に析出していない粒界にCO2が凝縮することによって,高い透過選択性が得られる可能性を示唆している。
VerticalモデルのNEMD計算結果のスナップショットを図11に示す。Verticalモデルでも粒界に選択的にCO2が吸着する様子が観察できる。興味深いことに,CO2の吸着量は結晶領域よりも粒界の方が多い。図12に示した濃度分布より,供給側から透過側までCO2の分布が確認できる一方,CH4の濃度は粒界があるにも関わらず増加していないことがわかる。これは,CH4よりもCO2の凝集エネルギーが大きいためだと考えられる。以上のことから,Verticalモデルでは粒界を透過するのは主にCO2だとわかる。粒界を含む膜モデルでの透過係数と分離係数の計算結果を表3に示す。HorizontalモデルではCH4の透過は観測されなかった。一方,VerticalモデルではCH4の透過がみられた。完全結晶(表2)と比較すると,粒界が存在することで透過係数は増加した。特にVerticalモデルでは2倍以上になった。一方,選択性をみてみるとVerticalモデルでは減少したものの,Horizontalモデルでは大幅に増加した。このことは,粒界におけるCO2の凝縮によってCH4の透過をブロックされるため,膜内部に粒界が存在していたとしても高い分子ふるい効果が発揮されると考えられる。これは,粒界の存在によって膜の性能が向上する可能性を示しており,完全結晶の膜よりも高い分離性能が得られることを示唆している。
表3. 多結晶のCHA膜におけるCO2分離性能 | 透過係数
[10-14 m3(STP) m/(m2∙Pa∙s)] | 選択性
αCO2⁄CH4 |
|---|
| CO2 | CH4 |
|---|
| Horizontal | 69 | — | ∞ |
| Vertical | 141 | 2.5 | 55 |
ハイシリカのCHA型ゼオライト膜は,カウンターカチオンをもたず,細孔容積が大きいため高透過性を有する。しかし,CO2/CH4混合系におけるCHA膜のCO2選択性は高圧になると低下することが報告されている1)。この要因として,Feed側におけるガスの濃度分極やゼオライト膜の結晶粒界の影響が考えられているが,その詳細については不明な点が多い。そこで,NEMD法を用いて,粒界をもつCHA膜の高圧条件下での分離性能について検討した17)。
膜モデルにはVertical型の膜モデルと,比較対象として完全結晶型のCHA膜モデルを採用した。混合ガスは等モル比でFeed側の出現層から0.5~8.0 MPaの圧力に応じて出現させた。NEMDから得られた透過係数および分離係数を図13に示す。CO2の透過係数は,完全結晶型,Vertical型どちらの場合も高圧下で減少した一方で,CH4の透過係数はどちらも増加した。これはKidaらの報告1)の傾向と一致する。完全結晶での濃度分布を解析したところ,高圧条件下で供給側の膜面付近のCO2濃度が減少し,CH4は増加することがわかった。したがって,膜表面に吸着したCH4分子がCO2の透過を阻害していると考えられる。高圧では,CH4の膜表面への衝突頻度が増加し,膜内に拡散するとCH4の分子数も増加する。一方CO2分子は,CH4分子の遅い細孔内拡散によって透過が抑制され,その結果として高圧になるほど透過係数は減少する。つまり,高圧でCHA膜のCO2透過係数が減少したのは,吸着よりも拡散の寄与が大きいことによるものだと考えられる。また,Vertical型では完全結晶膜と比べてCO2の透過係数の減少は緩やかである。これは,結晶粒界にCO2が選択的に分布するため,CH4による透過阻害の影響が小さくなったためだと考えられる。つまり,粒界の存在によって,高圧でのCO2透過係数の減少を抑制することができる。実際に図13に示されるように,Verticalモデルでは高圧での選択性の低下は小さくなっている。